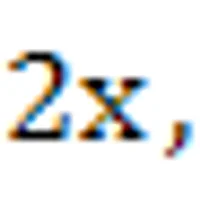[ 정보반스러운 생각 ]
이제 방금까지 했던 작업을 컴퓨터의 관점에서 생각해 보자. 종이에 적은 수식이야 얼마든지 존재할 수 있는 수학개념이지만, 컴퓨터의 입장에서는 어렵기 그지없다. 컴퓨터는 연속함수를 이해할 수 없다. 무한수열도 이해할 수 없다. 이미지프로세싱 1부에서 언급했던 '샘플링'이 필요한 것도 같은 이유에서이다.
"컴퓨터는 이산적이고(discrete) 유한한(finite) 데이터만 다룰 수 있기 때문이다"
컴퓨터는 생각보다 멍청해서, 연속함수는 띄엄띄엄한 점에서만 정의된 함수들로 이해시켜야 하고, 무한수열은 처음 몇 개를 제외한 뒷부분을 잘라서 유한수열로 만들어 주어야 비로소 컴퓨터가 이해할 수 있는 형태의 '데이터'가 된다.
함수들이 띄엄띄엄 정의되면 아래와 같이 된다. 0~π까지의 구간을 20개로 나누고, 그 중간중간에 점들을 찍었다. 컴퓨터가 다루는 데이터는 전부 이런 식으로 불연속적이다.

0~π까지의 구간을 N개로 나눈 경우를 생각해 보자. 각각의 나누어진 구간의 크기는 

N개의 점들 각각의 y좌표를 f0, f1, f2, … , fN-1 이라고 하면 얘네들도 "유한수열"이 된다. 그럼 결국엔 이 함수를 삼각함수들의 합으로 나타내기 위해 컴퓨터가 하는 일은 두 수열을 서로 이랬다 저랬다 바꾸는 작업이 되어버린다. 그림으로 나타내면 아래와 같다.
|
f0, f1, f2, … , fk , … , fN-1 |
the DCT → ← the IDCT |
C0, C1, C2, … , Cn , … , CN-1 |
이러한 두 배열 사이의 변환을 이산코사인변환 (DCT, Discrete Cosine Transform)이라고 한다. DCT는 처음 그래프에 점을 찍는 방법(나눈 구간의 중간에 찍느냐, 경계에 찍느냐 등등)에 따라 여러 종류가 있다. 그 중에서도 특별히 지금처럼 나눈 구간의 중간에 점을 찍은 경우, 왼쪽에서 오른쪽으로의 변환을 the DCT라고 하고 오른쪽에서 왼쪽의 변환을 the IDCT라고 한다. 여기서 I는 Inverse의 약자이다. 이제 이 둘을 the를 뺀 DCT, IDCT라 부르도록 하겠다.
또, f의 개수와 C의 개수가 N개로 서로 같다는 것에도 주목하자. 좌표평면 상의 3개의 점을 지나는 다항식을 찾기 위해선 2차식(항이 3개)이면 충분했다. 마찬가지로 좌표평면 상에서 N개의 점을 지나도록 하기 위해선 N종류의 cos함수면 충분하다. DCT의 결과가 입력과 똑 같은 길이 N의 배열이 되는 것이다. 이것을 염두에 두고, 먼저 DCT의 계산부터 알아보자. 아래와 같이 하면 fn으로부터 Cn을 구할 수 있다.

< DCT >
조금 복잡해 보일지도 모르겠다. 
Cn을 이용해서 함수 f를 다시 쓸 수 있다. 즉, 다음과 같이 쓸 수 있는 것이다.

첫 항에만 1/2이 들어간 것에 주의하자. k번째 점의 x좌표는 

< IDCT >
DCT와 IDCT의 식을 자세히 보면 둘이 닮은 것 같은 느낌이 들 것이다. Σ기호도 그렇고, cos함수 앞에 바꾸기 전 배열의 요소들이 곱해져 있는 것이나 cos함수 안에 들어가 있는 숫자도 비슷하다. 사실 이 둘은 DCT-2, DCT-3 이라고 불리는 여러 DCT들 중 하나이다. DCT의 종류에 대해서 더 자세한 건 부록으로 넘기도록 하고, 이것을 python으로 구현해 보는 연습을 해 보자.
|
import math |
위의 두 함수는 array를 입력으로 받아서 DCT와 IDCT를 수행해준다. 이제 여러분은 어떤 함수가 주어지더라도 그것들을 N개의 점으로 샘플링한 뒤 코사인 함수들의 합으로 나타낼 수 있을 것이다. Cn을 알아내기 위해, 위에서 정의한 DCT((1,2,3,4,5)) 를 호출해보자.
|
>>> DCT( [ 1, 2, 3, 4, 5 ] ) |
자. 과연 이 Cn들로 다시 fn을 그리면 어떤 모습일까? GrafEQ에서 그려본 결과는 아래와 같다. 1, 2, 3, 4, 5의 값을 차례로 갖는 그래프가 완성되었다.

< 
이 컨텐츠를 시작하면서 원하는 주파수에서만 정보를 쏙 뽑아서 사용하는 무선 기기들의 이야기를 했다. DCT와 라디오가 도대체 무슨 상관이 있는 걸까?

이 수식이 의미하는 바를 생각해 보자. A는 이 수식의 최대크기를 나타낸다. cos함수가 -1부터 1까지 변화하므로, 이 함수는 –A부터 A까지 변화한다. 여기서 A를 진폭(Amplitude)라고 한다. 그럼 ω는 무얼 의미할까? ω가 0이면 함수 값은 t와 상관없이 1이다. ω가 커질수록 함수의 모양이 어떻게 바뀌는지는 앞서 그림을 통해 봤다. ω가 바로 주파수(frequency)이다.
지금까지 DCT를 이용해 특정 함수를 삼각함수들의 합으로 나타내는 방법에 대해 다루었다. 이 때 '삼각함수들'은 
원하는 주파수 성분만 뽑는 기능은 물론이고, 입력 데이터 각각에서 어떤 주파수의 정보가 얼마나 많이 포함되어 있는지를 모두 판단할 수 있다. 음악을 즐겨 듣는 사람이라면, 플레이어의 Equalizer의 기능을 이용해 보았을 것이다. Equalizer는 낮은음과 높은음의 비중을 조절해서 음악의 느낌을 다양하게 바꾸어 준다. 이제 여러분은 Equalizer가 어떻게 동작하는지 이해할 수 있을 것이다. DCT를 이용해 각 주파수별 성분을 구한 뒤, 그것을 사용자의 설정대로 그것의 크기를 바꾼 뒤에, 다시 IDCT를 적용시키는 것이다.

< iTunes의 Equalizer >
이것이 바로 주파수 영역에서 신호를 처리하는 일반적인 방법이다. 음악 뿐만 아니라, 이미지(Image)에서도 똑같이 적용할 수 있다. 컨텐츠의 나머지 부분에서는, 아래와 같은 방식으로 이미지를 처리하는 방법을 다룰 것이다. 지금까지 수학분야 학습컨텐츠를 씩씩거리며 읽어온 여러분에게 심심한 사과의 말씀을 전한다. 이제부턴 정보컨텐츠스러워질 것 … 같다.
|
원본 |
→ |
DCT |
→ |
수정 |
→ |
IDCT |
→ |
결과 |
[ 연습문제 3 ]
( 문제 1 )
앞서 [ 0, π ]를 5개의 구간으로 나누고, 각 구간에서 1, 2, 3, 4, 5의 값을 가지는 함수를 cos함수들의 합으로 나타내는 방법을 알아보았다. 이번엔 [ 0, π ]를 10개의 구간으로 나누고, 각 구간에서 1, 2, 3, 4, 5, 0, 0, 0, 0, 0을 가지는 함수를 cos함수들의 합으로 나타내시오.
( 문제 2 )
f0, f1, f2, … , fN의 the DCT를 DCT(f0, f1, f2, … , fN-1) 이라고 나타내자. 다음을 증명하라.
-
상수를 곱해서 변환한 것과 변환한 것의 상수배는 같다.
DCT(c·f0, c·f1, c·f2, … , c·fN-1) = c·DCT(f0, f1, f2, … , fN) -
합해서 변환한 것과 변환해서 합한 것은 같다.
DCT(f0+g0, f1+g1, f2+g2, … , fN-1+gN-1) = DCT(f0, f1, f2, … , fN) + DCT(g0, g1, g2, … , gN)
이러한 성질을 만족하는 변환을 '선형'이라고 한다. DCT와 IDCT는 대표적인 선형 변환이다.
[목차] 이미지프로세싱 - 시작
[이전] 주파수 영역에서의 처리 - (3) 삼각함수의 합으로 나타내기 1
[다음] 주파수 영역에서의 처리 - (5) 2차원에서도 똑같이 해 보자