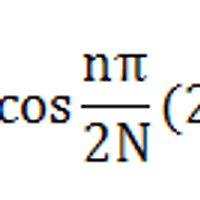주파수 영역에서의 처리 - (6) 주파수 영역에서 이미지 주무르기

자, 드디어 주파수 영역 이미지프로세싱을 맘대로 할 수 있게 되었다. DCT를 이용한 이미지프로세싱이 어떻게 이루어지는지 다시 확인하고 넘어가자.

원본

→

DCT

→

수정

→

IDCT

→

결과

원본 이미지에 DCT를 적용하여 주파수 스펙트럼을 추출한 다음, 그것을 수정하고 다시 IDCT를 적용하여 원하는 결과를 얻는 방법을 이용한다. 여러분은 [연습문제 4]에서 이러한 방식을 사용하는 아주 간단한 필터를 만들어 보았다.

여기서는 주파수 영역 처리에서는 대표적인 필터로 아래 세 가지를 꼽을 수 있는데, 여기서는 그 중 두 가지만 알아보도록 한다.

1. Low-pass Filter ( 저역 통과 필터 )

일반적으로 낮은 주파수 영역에는 전체적인 이미지의 윤곽에 대한 정보가 담겨 있고, 높은 주파수 영역에는 이미지의 세밀한 부분에 대한 정보가 담겨 있다. 낮은 주파수의 함수는 천천히 변화하고, 높은 주파수의 함수는 빨리 변화하기 때문이다.

Low-pass Filter는 말 그대로 낮은(Low) 주파수 영역의 정보만 통과(Pass)시키는 필터이다. 즉, 이미지에 이 필터를 적용하면 이미지의 세밀한 부분에 대한 정보는 지워지고 전체적인 윤곽에 대한 정보만 남게 된다. 결과적으로 이미지는 흐려지게 된다.

Low-pass Filter는 오디오에서 고음역의 불쾌한 잡음을 제거해 주는 Hiss Filter, 낮은 음역대의 정보를 우퍼(Woofer) 스피커에 전달하는 입체음향 시스템 등에서도 이용된다.

2. High-pass Filter ( 고역 통과 필터 )

High-pass Filter 역시 말 그대로 높은(High) 주파수 영역의 정보만 통과(Pass)시키는 필터이다. 이 필터에는 이미지의 세밀한 부분에 대한 정보들. 특히 갑자기 색이 많이 바뀌는 곳에 대한 정보가 포함되어 있어서, 경계선 검출 등의 분야에 널리 응용된다.

또한, 전자기기에서 Low-pass Filter회로와 High-pass Filter회로를 결합하면 특정 주파수 영역대만 통과시키는 Band-pass Filter를 만들 수 있는데, 이 필터를 이용하는 것이 원하는 주파수의 정보만 뽑아서 받아들이기 위한 핵심 원리이다.

3. Noise Reduction ( 잡음 제거 )

일상생활에서 발생할 수 있는 많은 현상은 주기적이다. 그네의 움직임, 시계추의 움직임, 심장박동 등 많은 현상들이 특정한 메커니즘에 의해 주기적인 성질을 갖게 된다. 정보처리에서 나타날 수 있는 잡음(Noise)도 규칙적인 패턴을 갖고 있는 경우가 많이 있는데, 이런 경우에는 잡음이 갖고 있는 주파수 성분을 제거해 줌으로써 쉽게 잡음을 없앨 수 있다.

[ Low-pass Filter – 저역 통과 필터 ]

Low-pass Filter가 무엇인지는 앞에서 미리 설명했다. 낮은 주파수만 통과하기 위해서는, "이것 이하의 주파수 정보만 통과시키겠다"라는 기준이 필요하다. 이것을 차단 주파수(Cutoff Frequency) 라고 한다. 이것을 C라고 나타내자.

이제 Low-pass Filter를 구현하는 방법 간단히 생각할 수 있다. 주파수 스펙트럼에서 C보다 큰 주파수 영역의 정보는 다 지워버리고 IDCT를 먹이면 되는 것이다. 2차원이므로, 주파수 스펙트럼 중에서 (0,0)으로부터 거리가 C보다 큰, 즉 n2+m2>C2인 부분에 대해서 Low-pass Filter를 적용하는 소스는 아래와 같다.

DCT()
for n in range(N):
for m in range(M):
if(n*n+m*m>C*C):
self.Result[n][m]=0

IDCT()

이것을 Ideal Low-pass Filter라고 한다. C를 10, 30, 50으로 했을 때 이 함수의 결과는 아래와 같다.

< Ideal Low-pass Filter 를 적용한 고양이 사진 >

예상했던 대로 이미지를 흐리게 하는 효과가 완성되었다. 고양이 사진의 크기는 373*473픽셀인데, 반지름이 50인 사분원에 있는 정보만으로도 이미지의 윤곽이 거의 다 나타났다. 이러한 특징으로 인해, DCT는 JPEG압축 기술에서도 핵심적으로 이용된다.

< 처음 이미지와 주파수 스펙트럼, C=100인 위치가 표시되어 있음 >

< Ideal Low-pass Filter를 적용한 이미지와 그 주파수 스펙트럼 (C=100) >

Ideal Low-pass Filter는 주파수별로 주파수 스펙트럼에 아래와 같은 함수를 곱했다고 생각하면 된다. 이것을 필터 함수(Filter Function)이라고 한다.

< Ideal Low-pass Filter의 필터 함수 >

음, 그런데 한가지 이상한 점이 보인다. 고양이 얼굴 뒷부분의 벽에 원본 이미지에서와 달리 울퉁불퉁한 무늬들이 보인다. 이러한 점들은 왜 생긴 것일까? 코사인 급수를 나타낸 그래프를 다시 열어 보자.

< 코사인 급수에서 링잉(Ringing)이 일어난 모습 >

그래프가 직선에 점점 가까워지고 있긴 하지만 직선 아래위로 계속 오르락내리락하고 있는 모습을 확인할 수 있다. 직선이 되려면 무한 개의 삼각함수를 더해야 하는데, 이 그래프에선 처음 몇 개만 그렸기 때문에 이런 현상이 나타났다.

마찬가지로 Ideal Low-pass Filter도 "처음 몇 개의 정보만" 반영했기 때문에 울퉁불퉁한 패턴이 나타나게 된다. 이러한 현상을 링잉(Ringing)이라고 하고, 이것을 없애기 위해 고안된 새로운 필터가 있는데, 이것이 바로 Buttorworth Filter이다. 이 필터는 주파수 ω의 정보에 대해, 다음과 같은 필터 함수를 적용시킨다. 여기서 n은 자연수이고, n이 커질수록 점점 Ideal Low-pass Filter에 가까워진다.

< Buttorworth Low-pass Filter 의 필터 함수 >

< Ideal Low-pass Filter(왼쪽)와 Butterworth Low-pass Filter(n=1, 오른쪽)의 결과 비교>

구현은 여러분에게 맡기고, 여기선 Ideal과 Butterworth의 차이점을 확인해 보자. Low-pass Filter를 사용하였더니 링잉이 나타나지 않은 것을 확인할 수 있다.

이외에도 몇 가지 다른 종류의 필터도 고안되어 있으나, 이 교재에서는 여기까지만 다루도록 하겠다.

[ High-pass Filter – 고역 통과 필터 ]

High-pass는 앞서 설명했던 대로, 높은 주파수 영역은 이미지의 세밀한 부분에 대한 정보를 담고 있으며, 경계선 검출 등에 사용된다고 설명했었다.

High-pass Filter를 구현하는 방법은 Low-pass에서와 거의 똑같다. 단지 Low-pass Filter에서 작은 주파수에 대해 적용하던 것을 높은 주파수에 대해서 적용하면 된다. High-pass Filter에도 Ideal과 Buttorworth가 있으며, 각각의 필터 함수는 1에서 Low-pass의 필터함수를 빼면 된다. 그림으로 나타내면 아래와 같다.

< Ideal High-pass Filter 의 필터 함수 >

< Buttorworth High-pass Filter의 필터 함수 >

고양이 사진에 두 종류의 High-pass Filter를 적용해 보자. 이 때, 높은 주파수 영역의 정보는 낮은 주파수 영역에 담긴 정보를 제외한 '나머지 부분'의 세밀한 정보를 갖고 있기 때문에, 그것만 복원했을 때 음수의 값을 가질 수도 있다. 그래서 결과 이미지의 픽셀값에 128 (회색)을 더해서 음수로 표현나는 정보까지도 눈으로 확인할 수 있도록 했다.

< Ideal High-pass Filter(왼쪽)와 Butterworth High-pass Filter(n=1, 오른쪽)의 결과 비교>