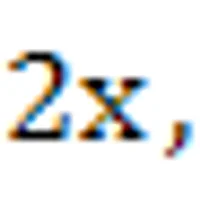여기에는 연습문제와 상관없이, 이 컨텐츠에서 다루었던 주제들에 관해 더 알고 싶어하는 이들을 위해 몇 가지 설명을 추가했다. 사실 자세히 다루려면 너무 분량이 많아지지만 꼭 알려주고 싶은 내용들이다. 주파수 영역에서의 정보처리가 얼마나 다양한 분야에서 이용되고 있는지 실감할 수 있도록, 다양한 자료들을 단편적으로 제시하고, 더 알고싶은 사람들을 위해 링크, 팁 등을 제시했다.
[ 코사인 급수 만드는 법, DCT식의 유래 ]
[0, π]에서 정의된 일반적인 함수를 코사인 급수로 만들기 위해서는 다음과 같이 하면 된다. 적분식을 처음 본다면, "

< 코사인 급수의 계수를 구하는 공식 >
이산코사인변환에서 구한 은 이것을 수치적으로 계산한 것에 해당한다. 0~π에 해당하는 구간을 N개로 나누고, 나눈 부분마다 사각형을 만들어서 그래프 아랫부분의 넓이를 근사하는 것이다. k번째 막대의 높이는 




[ 푸리에 급수 ]
코사인 급수는 항상 y축에 대칭이어야만 했다. 주기가 2π인 함수들 중에서도 이런 경우는 굉장히 특수한 경우이기 때문에 많은 제약이 따른다. 일반적인 주기함수를 삼각함수의 합으로 나타내기 위해서는 사인과 코사인 함수를 함께 이용해야 하는데, 이것을 푸리에 급수(Fourier Series)라고 한다. [-π, π]에서 정의된 함수 



< 푸리에 급수의 계수를 구하는 공식 >
코사인 급수 공식에서 사인함수에 관련된 항 몇 개만 추가되었다. 이 공식을 유도하기 위해서는 몇 가지 미적분학 지식이 필요한데, 관련 사이트 몇 개를 링크하도록 하겠다.
사실 내가 고등학교에 다닐 때, 푸리에 급수라는 게 너무나도 신기해서, 배우고 싶었지만 가르쳐 주는 사람이 없었다. 하지만 이제 여러분에게 이 학습컨텐츠를 통해 당시의 내가 정말 배우고 싶었던 내용들을 알려주고 있다는 것에 뿌듯해 하고 있다. 과연 얼마나 이걸 배우고 싶어하고 있을 진 모르겠지만-_-a
(영어) http://www.sosmath.com/fourier/fourier1/fourier1.html
(한글) http://cc.kaist.ac.kr/2006spring/gct561/lectures/14-1-Fourier%20Series.doc
푸리에 급수는 삼각함수들이 가지는 특징들 때문에 편미분방정식을 푸는 데에도 유용하게 사용된다. 대표적인 예로는 열평형 상태에 있는 물체의 온도분포 구하기와 같은 것이 있다. 몇 페이지 아래에서 조금 더 자세하게 설명한다.
[ 이산푸리에변환 ]
푸리에 급수는 코사인급수와 달리 [-π, π]구간에서 정의된 함수를 사용했으며, 코사인과 사인함수를 모두 사용했기 때문에 결과도 Cn과 Dn의 두 가지였다. 이 두 가지 결과를 Cn+iDn 과 같이 코사인함수의 계수를 실수부분으로, 사인함수의 계수를 허수부분으로 가지는 복소수로 나타낼 수 있다. 이와 같은 개념으로 이산푸리에변환(DFT, Discrete Fourier Transform)이 정의된다.
고양이 사진에 DFT를 적용하면 아래와 같이 된다. 아래 이미지는 DFT 결과로 얻은 복소수의 절대값만 이미지로 나타낸 것이다.

< DFT 공식 >

< DFT의 결과 >
이산코사인변환(DCT)과는 달리 밝은 점이 중앙에 집중되어 있는 것이 보인다. DFT결과 이미지에서, 낮은 주파수 영역은 중앙에 가까이 있는 부분이고, 높은 주파수 영역은 중앙에서 멀리 떨어진 부분이다.
복소수를 이용하는 것으로, y축에 대칭인 형태를 하고 있지 않는 주기함수에 대한 결과가 DFT 의 주파수 스펙트럼에 정확하게 나타날 수 있다. 6장에서 언급만 하고 넘어갔던 노이즈 제거(Noise Reduction)에서는 DFT를 이용하는 것이 더 바람직한데, 이것은 노이즈가 y축에 대칭일지 아닐지는 알 수 없기 때문이다.
이 컨텐츠에서 DFT를 사용하지 않은 이유는 이미지프로세싱에서 DCT가 더 많이 이용되기 때문이기도 하지만, 개념의 전개에서 복소수에 대한 내용을 다루고 싶지 않아서였다. 복소수를 이용하면 좀더 일반적인 주기함수에 대한 처리를 할 수 있기 때문에, 앞서 예로 든 이퀄라이저와 같은 정보처리에서는 DFT를 더 흔히 사용한다.
[ 여러 가지 이산코사인변환 ]
앞서 이산코사인변환(DCT)에는 여러 가지 종류가 있다고 이야기했었다. 크게 네 가지 종류가 있는데, 그림으로 나타내면 아래와 같다.

< 여러 가지 DCT >
DCT-2가 4장에서 설명했던 DCT이고, DCT-1이 5장과 6장에서 다루었던 DCT알고리즘이다. DCT-1의 역은 DCT-1이며, DCT-2의 역은 DCT-3이고, DCT-4의 역은 DCT-4이다.
이 중 JPEG압축에 사용되는 것은 DCT-2이고, 이 교재에서 DCT-1을 이용한 것은 Numpy에서 제공하는 FFT함수를 이용하기 위해 불가피했기 때문이다. DCT-1~4의 식은 차례로 아래와 같다. 이 컨텐츠에서 제공했던 식은 cos함수의 계수를 맞추기 위해 앞에 상수(2/N)가 곱해져 있었다.




출처 : 위키백과 (http://en.wikipedia.org/wiki/Discrete_cosine_transform)
[ 푸리에 변환의 네 가지 종류 ]
푸리에 급수는 연속인 함수를 삼각함수들의 합으로 나타내는 것이었고, 이산푸리에변환은 불연속인 함수를 삼각함수들의 합으로 나타내는 것이었다. 그런데, 주파수 영역의 계수들은 모두 불연속적이었던 것을 기억하자. 연속함수 f(x)에 몇 개의 점을 찍어서 fn을 만들었다. 반대로 주파수 스펙트럼의Cn을 연속함수 C(ω)로 만들 순 없을까?
주파수 스펙트럼이 불연속적인 이유는 2π마다 같은 값을 가지는 코사인함수는 반드시 의 꼴을 만족해야 했기 때문이었다. 주기를 갖고 있지 않는 함수에 대해서라면, 이것을 연속적인 주파수 스펙트럼으로 표현할 수 있을 것 같다. 이것이 바로 연속푸리에변환(Continuous Fourier Transform)의 개념이다. 어떤 함수 f(x)의 연속푸리에변환은 아래와 같이 구한다.

여기서 
푸리에 급수를 이산푸리에변환으로 근사한 것처럼, 푸리에 변환에서 f(x)를 불연속적인 값으로 바꾸면 이산시간푸리에변환(Discrete-Time Fourier Transform)이 완성된다.

이렇게 해서, 푸리에 변환은 모두 네 가지 종류가 된다. 데이터가 시간영역(Time Domain)과 주파수 영역(Frequency Domain)에서 연속적인지 이산적인지에 따라 나뉘는데, 이것을 표로 나타내면 아래와 같다.
|
시간 영역 주파수 영역 |
연속적 |
이산적 |
|
연속적 |
연속푸리에변환 |
이산시간푸리에변환 |
|
이산적 |
푸리에 급수 |
이산푸리에변환 |
[ 빠른 푸리에 변환 ]
앞에서 빠른 푸리에 변환(FFT, Fast Fourier Transform)을 이용하면 DFT를 n log n 에 비례하는 시간만에 계산할 수 있다고 하였다. 1942년에 고안된 이 알고리즘은 길이가 N인 데이터를 두 개의 데이터로 분할하여 DFT를 적용하고 다시 그것을 혼합하여 결과를 만드는 분할정복법(Divide and Conquer)을 이용한다. 데이터를 두 개로 나누어 정렬한 뒤 그것을 다시 혼합하는 합병정렬과 비슷한 원리이다. FFT의 원리를 개략적으로만 알아 보자.


행렬은 마치 구구단 표처럼 생겼다. 가운데의 행렬을 

위 식에서 2x2 행렬은 각각의 행렬을 상하좌우로 연결한 행렬을 뜻한다. I는 대각선의 원소만 1이고 나머지 원소는 0인 항등행렬이다. P는 짝수행이 위쪽, 홀수행이 아래쪽에 바꾸어 주는 순열행렬(Permutation Matrix)이고, D는 ω에 관한 정보를 담고 있는 대각행렬이다.
결국 푸리에 변환은 에 행렬 

FFT가 없었더라면 고양이 사진 하나를 변환하는 데에 수십 분이 걸렸을 것이고, 푸리에 변환을 이용한 응용결과 조차 없었을 것이다. MIT교수 Gilbert Strang은 FFT를 "우리 세대의 가장 아름다운 알고리즘"으로 묘사했다. FFT의 정확한 유도 방법이 알고 싶은 사람은, 아래 링크를 이용하자.
http://huniv.hongik.ac.kr/~swsyoon/research/FFT1.htm
[ 수리물리학에의 응용 ]
물리학에서는, 특정한 미분방정식(Differential Equation)과 경계조건(Boundary Condition)을 만족하는 필드(Field)를 구하는 문제를 자주 접할 수 있다. 대표적인 예로, 균일한 전기장 안에 전도체가 들어 있을 때 유도되는 전기장을 구한다든지, 경계면의 온도가 일정하게 유지되는 방의 온도 분포를 구한다든지 하는 것들이다. 첫 번째 경우에서는 도체 외부의 전기장의 라플라시안(Laplacian)이 0이 되는 것이 미분방정식이고, 도체 표면에서의 전위가 균일하다는 것이 경계조건이다. 두 번째 경우엔 열전도방정식이 미분방정식에 해당하고, 표면에서 유지되는 온도가 경계조건에 해당한다.
이러한 문제들을 해결할 때는, 구하고자 하는 해가 푸리에 급수라고 가정한 뒤 미정계수법을 사용하게 된다. 우선 계수를 정하지 않은 채 푸리에 급수로 답을 적은 뒤, 경계조건을 대입하여 계수를 결정할 수 있다. 이 때, F(x,y)꼴의 해를 X(x)Y(y)와 같이 각 변수들만의 함수들의 곱으로 표현하는 변수분리(Separation of Variables)라는 방법이 이용된다.
하지만 손으로 이것을 계산할 수 있는 경우는 도체가 완벽한 구(Sphere)이거나 방이 완벽한 직육면체일 때처럼 이상적인 경우 뿐이고, 대부분의 경우 수치적인 계산에 의존해야 한다. 이 때 푸리에 변환이 필수적으로 사용된다. 아래는 수치적으로 방의 열평형상태를 구한 이미지이다.

< 벽의 온도가 일정하게 유지되는 방안의 온도 분포를 수치적으로 구한 모습 >
푸리에급수가 물리학에서 응용되는 분야에 관심이 많은 학생은, 수리물리학이나 전자기학의 전공도서에서 관련된 방법을 찾아볼 수 있다. 하지만 편미분방정식에 대한 이해가 불가피해서 난이도가 좀 있다;
[ 필터 디자인 ]
지금까지는 DCT나 DFT를 컴퓨터상에서 직접 계산하는 것만 다루었다. 이것을 디지털 필터 (Digital Filter)라고 한다. 하지만 라디오를 비롯한 무선기기에서는 저항, 축전기, 코일 등의 소자들이 가지고 있는 물리학적인 성질을 이용하여 필터를 사용하기도 한다.
저항은 일반적으로 전류나 전압의 변화에 상관없이 작동하며, 전압과 전류의 비율을 조절하는 역할을 한다. 하지만 축전기는 빠르게 변화하는 전압에는 반응하지만 느리게 바뀌는 전압에는 끊어진 회로처럼 반응한다. 코일의 경우 축전기와는 반대로 느리게 변화하는 전압에는 그냥 전선이 이어진 것처럼 반응하지만, 빠르게 변화하는 전압에는 코일 내부에 생긴 자기장에 의해 방해를 받는다. 이러한 원리를 이용하여 만든 필터를 아날로그 필터(Analog Filter)라고 한다. 디지털 필터는 이산적으로 샘플링된 데이터를 이용하기 때문에 생기는 오차가 발생하고, 아날로그 필터는 물리적인 측정오차나, 소자들의 비선형성(nonlinearity)에 의한 오차가 발생한다.
다음은 저항, 축전기, 코일 등을 이용하여 필터를 만든 예이다.
< 축전기와 저항을 이용한 Low-pass Filter (왼쪽)와 High-pass Filter(오른쪽) >
< 저항, 축전기, 코일을 이용하여 만든 Band-pass Filter의 예 >
디지털한 방법을 이용하든, 아날로그한 방법을 이용하든, 주파수라는 개념이 정보화시대에 갖는 중요성은 상당하다. 전자기기에서 사용되는 이러한 필터에 대해 자세히 공부하고 싶은 사람은 전자공학과로 진학하길 권유한다-,-;
http://www.icat.or.kr:3000/dsp/ (디지털 신호처리에 관한 한글 사이트)
http://ccrma.stanford.edu/~jos/filters/Analog_Filters.html (아날로그 필터)
[ 맺음말 ]
이 컨텐츠가 이미지프로세싱에 관련된 것이란 게 무색할 정도로 다양한 분야의 내용을 많이 담았다. 지금까지 다룬 내용은 컴퓨터공학과, 전자공학과, 수학과 등에서 배우는 2, 3학년 과정의 과목들과 긴밀하게 연결된다.
DCT와 DFT는 대표적인 선형변환(Linear Transform)이며, 이러한 변환에 대한 자세한 성질은 선형대수학(Linear Algebra, 수학과 2학년)에서 다루게 된다. 푸리에 변환과 관련된 수학적 개념과 응용은 응용해석학(Applied Mathematical Analysis, 수학과 2학년)이나 수리물리학(Mathematical Physics, 물리학과 2학년)에서 자세히 다루게 된다. 또한, 주파수 영역에서의 신호처리에 관한 내용은 신호 및 시스템(Signal & Systems, 전자공학과 2학년) 과목에서 다루게 되고, 통신공학 (Communication Systems, 전자공학과 3학년), 제어시스템공학(Control System Engineering, 전자공학과 3학년) 등에서 다양하게 응용된다.
컴퓨터 그래픽스라는 분야를 제외하고서도 셀 수 없이 많은 분야의 기초가 되는 내용들을 여러분에게 알려주고 싶었다. 이 컨텐츠가 앞으로 이공계 대학으로 진학할 여러분에게 무언가 방향을 제시해 주길 바라고 있다면 너무 큰 기대이려나ㅎ
이번에도 최대한 간단명료하게 쓰려고 했지만 40페이지를 넘고 말았다. 코딱지만한 스크롤바의 네모가 나로 하여금 미안한 마음을 들게 하고 있다. 계획을 세울 땐 열 몇 페이지면 완성할 수 있을 것 같았는데, 그림을 많이 넣고 자세하게 설명을 하느라 분량이 계속해서 길어졌고; 일주일 밤낮을 컨텐츠 만드는 데 사용했다. 하지만 이 컨텐츠를 재미있게 읽어준 학생이 한 명이라도 있다면, 행복할 것 같다^ㅡ^
[목차] 이미지프로세싱 - 시작
[이전] 주파수 영역에서의 처리 - (6) 주파수 영역에서 이미지 주무르기
[다음] (없음)